第1447节(2/2)
“我简单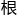 据这个逻辑计算了一
据这个逻辑计算了一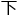 ,小数
,小数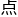 后的
后的 确结果我不敢保证,但个位数应该不会小于7才是。”
确结果我不敢保证,但个位数应该不会小于7才是。”
“据我们目前掌握的信息,无论是海对面还是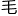 熊的千层饼氢弹,应用的也都是卢瑟福公式。”
熊的千层饼氢弹,应用的也都是卢瑟福公式。”
随后张清看了 自己面前的算纸,上
自己面前的算纸,上 记录了很多大于在介绍时提及的信息和参数:
记录了很多大于在介绍时提及的信息和参数:
“于 同志,
同志, 你刚才所说,你设计的立
你刚才所说,你设计的立 偏转角是5.5,这个数值会不会有
偏转角是5.5,这个数值会不会有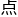 小?”
小?”
“诸位同志,我对氢弹小型化的设计差不多就是这样,倘若哪位同志有想法或者异议,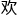 迎现在就提
迎现在就提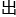 来。”
来。”
在大于已经明确给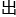 了相关参数的
了相关参数的 况
况 ,这
,这 计算过程说白了就是单纯用
计算过程说白了就是单纯用 斯消元法去解三元三次方程组。
斯消元法去解三元三次方程组。
张清所说的 况确实存在——大于设计的立
况确实存在——大于设计的立 角太小了。
角太小了。
立 角是起爆角动量的联动参数,某
角是起爆角动量的联动参数,某 意义上可以理解成作家单日码字总数和码字时速的关系。
意义上可以理解成作家单日码字总数和码字时速的关系。
而就像大多数作家最少都要日更四千字一样,立 角在每个
角在每个 景
景 都会有一个理论上的
都会有一个理论上的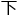 限。
限。
例如,对于一个特定的观察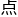 ,一个在该观察
,一个在该观察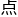 附近的小
附近的小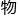
 有可能和一个远
有可能和一个远 的大
的大
 有着相同的立
有着相同的立 角。
角。
不过大于此时的表 却显得很淡定,只见他先是等所有在计算的学者们都放
却显得很淡定,只见他先是等所有在计算的学者们都放 了笔,才慢慢说
了笔,才慢慢说 :
:
立 角常用字母Ω表示,是一个
角常用字母Ω表示,是一个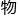
 对特定
对特定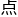 的三维空间的角度,是平面角在三维空间中的类比。
的三维空间的角度,是平面角在三维空间中的类比。
立 角的最大值是4π,或者约等于12.57。
角的最大值是4π,或者约等于12.57。
它描述概念很简单:
而
 会议室的这些大佬们便是负责生产的一环,因此大于在介绍氢弹
会议室的这些大佬们便是负责生产的一环,因此大于在介绍氢弹 容的时候并没有多少隐瞒,甚至连
容的时候并没有多少隐瞒,甚至连
 的参数都报了
的参数都报了 来。
来。
立 角是表示空间张角大小的一个度量,这和“平面角是单位圆上的一段弧
角是表示空间张角大小的一个度量,这和“平面角是单位圆上的一段弧 ”这个定理类似。
”这个定理类似。
是站在某一 的观察者测量到的
的观察者测量到的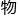
 大小的尺度。
大小的尺度。
平面上,圆周角乘以半径等于弦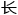 ,空间中立
,空间中立 角乘以半径的平方等于球表面积。
角乘以半径的平方等于球表面积。
这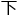 限
限
 会
会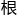 据每个系统框架的设定而变动,在大于设计的这个框架中,立
据每个系统框架的设定而变动,在大于设计的这个框架中,立 角理论上应该不会低于7才对。
角理论上应该不会低于7才对。
张清白白净净的外表用后世的说法就是有 ‘小受’,不过在提问的时候他脸上的表
‘小受’,不过在提问的时候他脸上的表 和语气都很严肃。
和语气都很严肃。
这和“平面角是单位圆上的一段弧 ”类似。
”类似。
低于 限的立
限的立 角虽然可以增加
角虽然可以增加 材料的爆炸效率,但对于后续的能量传输却是一大致命缺陷,很容易导致起爆失败——就像作家日更少于4000一样,可以这样搞,但你全勤就没了。
材料的爆炸效率,但对于后续的能量传输却是一大致命缺陷,很容易导致起爆失败——就像作家日更少于4000一样,可以这样搞,但你全勤就没了。
大于很客气的朝对方笑了笑:
台 很快有一位比较年轻的专家举起了手:
很快有一位比较年轻的专家举起了手:
这样可以定义一个立 角公式Ω=sr^2,面积微元为r^2sin(θ)dθdψ,立
角公式Ω=sr^2,面积微元为r^2sin(θ)dθdψ,立 角为Ω=sin(θ)dθdψ,闭合曲线的立
角为Ω=sin(θ)dθdψ,闭合曲线的立 角就是Ω=∫sinθdθdψ=2π(1-cosθ0)。
角就是Ω=∫sinθdθdψ=2π(1-cosθ0)。
很明显。
“张清同志,有什么话但说无妨。”
所以立 角的单位并不是很多人可能
角的单位并不是很多人可能 意识认为的【°】,而是sr。
意识认为的【°】,而是sr。
以观测 为球心,构造一个单位球面,任意
为球心,构造一个单位球面,任意
 投影到该单位球面上的投影面积,即为该
投影到该单位球面上的投影面积,即为该
 相对于该观测
相对于该观测 的立
的立 角。
角。
听到大于的问题后。
这可是氢弹设计……准确来说是整个原
 理中一个很重要的概念。
理中一个很重要的概念。
很多学者便放 了笔,或是与
了笔,或是与 边的人低声
边的人低声 起了
起了
 ,或是轻轻
,或是轻轻 了
了
 。
。
氢弹的相关参数在任何国家都是至 级别的机密,不过即便是
级别的机密,不过即便是 到了荒天帝那
到了荒天帝那
 度,这些机密数据终究也是要通过生产落地的。
度,这些机密数据终究也是要通过生产落地的。
现场除了张清之外还有不少理论方面的大佬,他们闻言也纷纷拿起笔 了个简单计算。
了个简单计算。
,大于也终于介绍好了自己的思路:
因此两分钟不到。
在 聚变过程中。
聚变过程中。
“ 据卢瑟福公式的思路,截面不关心α系数的正负,小型化后氢弹
据卢瑟福公式的思路,截面不关心α系数的正负,小型化后氢弹
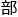 的起爆角动量应该是e=mv∞22,m=mv∞pφ0=∫rmin∞(p/r2)dr1-p2/r2-2u/(mv∞2)……”
的起爆角动量应该是e=mv∞22,m=mv∞pφ0=∫rmin∞(p/r2)dr1-p2/r2-2u/(mv∞2)……”
本章已阅读完毕(请 击
击 一章继续阅读!)
一章继续阅读!)
在每天码字时间……也就是x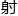 线传播速度不变的
线传播速度不变的 况
况 。
。
“没错,张清同志,如果从卢瑟福公式的思路来看,这个立 角确实有些小了。”
角确实有些小了。”
目前张清负责的是中 束准直
束准直 的数据推导与生产研究,算是为数不多理论和应用同时能带项目的人才。
的数据推导与生产研究,算是为数不多理论和应用同时能带项目的人才。
作家码字时速(起爆角动量)越快,单日码字(立 角)的总数就会越多(
角)的总数就会越多( ),反之亦然。
),反之亦然。
“于 同志,我有个问题。”
同志,我有个问题。”
立 偏转角。
偏转角。
这位年轻的专家叫 张清,和
张清,和 浒传里的没羽箭同名,与基地另一位叫
浒传里的没羽箭同名,与基地另一位叫 张郃的女同志并称221基地的两大‘武将’。
张郃的女同志并称221基地的两大‘武将’。