第1559节(2/3)
只见他拿起笔,很快在纸上写 了那
了那 方程:
方程:
没结果归没结果,徐云倒也不至于一 收获都没有。
收获都没有。
因为徐云在期间发现了温度和类似层状结构的表达式,显然是某
 理现象的新媒介,而且多半和晶
理现象的新媒介,而且多半和晶 有一定关系。
有一定关系。
剩余的两个阶段徐云也 了一些零散时间研究过,奈何由于能力问题,他一直没有找
了一些零散时间研究过,奈何由于能力问题,他一直没有找 正确的解——如今徐云的能力大概在教授之上院士之
正确的解——如今徐云的能力大概在教授之上院士之 ,而这两个阶段中最简单的第二阶段也属于菲尔兹奖……也就是数学最
,而这两个阶段中最简单的第二阶段也属于菲尔兹奖……也就是数学最 奖的难度层次了。
奖的难度层次了。
(1-η2)(z±(n=5)±3):(k(z±3)√120)k/[(1/3)k(8+5+3)]k(z±1)≤1(z±(n=5)±3);
至少……徐云得和老 见过一次面,才有可能讨论那事儿。
见过一次面,才有可能讨论那事儿。
本章尚未读完,请 击
击 一页继续阅读---->>>
一页继续阅读---->>>
当然了。
譬如在解方程的过程中他就发现,第二阶段的最终成果应该与某个机理有关。
他有一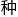 预
预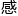 ,第二阶段的这个未必能够给他带来多少奖项上的荣誉,但很可能会产生某
,第二阶段的这个未必能够给他带来多少奖项上的荣誉,但很可能会产生某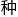 更大的影响力。
更大的影响力。
换而言之。
{qjik}k(z/t)=[xak(z±s±n±p),xbk(z±s±n±p),……,xpk(z±s±n±p),……}∈{dh}k(z±s±n±p)……
最后的一个公式……或者说一个数值为:
随后徐云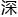
 一
一 气,将注意力放到了面前的算纸上。
气,将注意力放到了面前的算纸上。
其中第一阶段是一到三行,通过∑(jik=s)n(jik=q)(xi)(wj)可以确定曲面与经线成了某个定角,从而假设定模型λ=(a,b,π),以及观测序列o=(o1,o2,……,ot)。
方程前三分之一的 容,后
容,后 最少还有两个阶段没有被解
最少还有两个阶段没有被解 来。
来。
{qjik}k(z/t)=∑(jik=s)n(jik=q)(xi)(wj)(rk);(j=0,1,2,3……;i=0,1,2,3……;k=0,1,2,3……)
w(x)=(1-η[xy]2)k(z±s±n±p)/t{0,2}k(z±s±n±p)/t{w(x0)}k(z±s±n±p)/t……
(1-ηf2)(z±3)=[{k(z±3)√d}/{r}]k(z±m±n±3)=∑(ji=3)(ηa+ηb+ηc)k(z±n±3);
4d/b2=4(√(d1d2))2/[2d0]2=√(d1d2)/[d0]=(1-η2)≤1……
即便徐云的猜测有误也没事儿,徐云手上还有冷聚变的相关研究 打底呢。
打底呢。
当然了。
le(sx)(z/t)=[∑(1/c(±s±p)-1{nxi-1}]-1=n(1-x(p)p-s)-1。
所以在得知了自己答辩委员会的评审阵容之后,徐云便把主意打到了第二阶段的成果上。
 照孤
照孤 粒
粒 的
的 况来推测,后两个阶段应该也有对应的……唔怎么说呢,应该描述为有对应的
况来推测,后两个阶段应该也有对应的……唔怎么说呢,应该描述为有对应的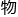 理现象?
理现象?
这是一个标准的正则化组合系数和解析延拓方程组,涉及到了无限多层次的对称与不对称曲线曲面的圆对数与拓扑。
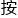 照上面的逻辑推导,就可以得
照上面的逻辑推导,就可以得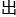 孤
孤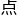 粒
粒 的概率轨
的概率轨 。
。
至于第三阶段的那个神秘比值……徐云敢肯定,它一定是一项可以震动世界的结果,保守估计都和相对论是同一级的,属于徐云目前哪怕 掉所有思维卡都不可能
掉所有思维卡都不可能 及的
及的 度。
度。
本章未完,点击下一页继续阅读